Exploring the Algebraic Intricacies of 58.2x^2 – 9x^2 and 5 – 3x + y + 6

Introduction:

58.2x^2 – 9x^2 and 5 – 3x + y + 6 – Algebraic expressions are powerful tools in mathematics, offering a concise way to represent complex relationships and phenomena. This article will explore the particulars of the expression 58.2x^2 – 9x^2 and 5 – 3x + y + 6. By breaking down each expression, simplifying where possible, and exploring potential relationships, we aim to shed light on the mathematical beauty within these seemingly abstract symbols.

Section First: Understanding the Component 58.2x^2 – 9x^2

The 58.2x^2 – 9x^2 comprises two terms, each involving the variable x raised to the power of 2. By combining these components, we arrive at the simplified form 49.2x^2. This result highlights the importance of recognizing and combining like terms in algebraic expressions. On the other side of the semicolon, we encounter 5−3x+y+6. This expression contains a mix of constants and variables. First, let’s discuss graphically below.

The first expression involves two terms: 58.2x^2 and -9x^2. To simplify, combine the terms:

58.2x^2 -9x^2

Combine the coefficients of the x^2 terms:

58.2x^2 -9x^2 = [58.2-9] x^2

= 49.2x^2

So, the simplified form of the first expression is 49.2x^2.

Section Second: Analyzing 5 – 3x + y + 6

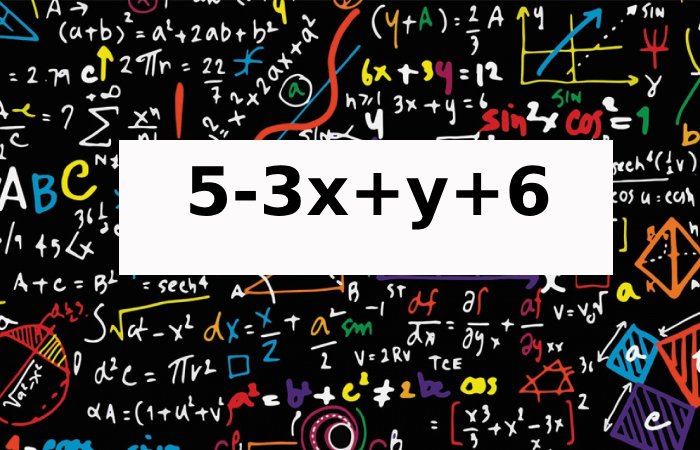
The second expression, 5 – 3x + y + 6, is composed of four terms: 5, – 3x + y and 6. While these terms might appear dissimilar, each serves a unique purpose. Combining the constants in the expression (5 and 6), we get 5+6=11. It leaves us with 11−3x+y. The expression remains simplified, and we are now ready to explore potential relationships between 49.2x^2 = 11−3x+y.

5 – 3x + y + 6

Combine the constant terms:

5+6 = 11

So, the simplified form of the second expression is 11−3x+y.

Now, if we put both simplified expressions together with a semicolon:

49.2x^2 = 11−3x+y

Section Third: Exploring Relationships

At first glance, the two expressions seem independent, each standing independently. However, the richness of algebra often lies in the relationships between different expressions. To explore potential connections, let’s consider various scenarios.

Scenario 1: Equating the Expressions

49.2x^2 = 11−3x+y

This scenario involves setting the two expressions equal to each other. By doing so, we create an equation that allows us to explore values of x and y that satisfy this relationship. Solving such equations can lead to insights into the connection between the two expressions.

Scenario 2: Graphical Representation

Creating graphs for both expressions and examining their behavior can provide visual clues about any intersection points or patterns. Graphing can enhance our understanding of how changes in x and y affect the overall expression.

Scenario 3: Factoring and Simplification

If applicable, exploring common factors or simplification techniques may reveal hidden relationships. Factoring involves expressing an expression as the product of its factors, potentially allowing us to cancel out standard terms.

Applications and Real-World Context

Polynomial expressions and equations find applications in various real-world scenarios. From physics to economics, these mathematical tools provide a framework for understanding and modeling complex systems.

Physics Example

Consider the motion of a projectile. The height (y) of the projectile at a given time (x) might be modeled by a quadratic equation involving terms similar to 49.2x^2.

y = 49.2x^2+h0

​Where ℎ0 represents the initial height. In this case, 11−3x+y could represent additional factors affecting the height, such as air resistance or external forces.

Economics Example

In economics, polynomial equations can model various situations, such as profit maximization or cost functions. The expressions 49.2x^2 and 11−3x+y might represent different components of a profit equation, where x could signify the quantity of a product sold, and y represents additional factors affecting profit.

Conclusion

In exploring the polynomial expressions 58.2x^2 – 9x^2 and 5 – 3x + y + 6, we’ve uncovered their simplifications and considered potential relationships. Mathematics offers a versatile toolkit for unraveling complexity, whether they are part of an equation, represent different terms in a larger polynomial, or are connected through dependent variables.

The real-world applications of polynomial expressions demonstrate the importance of these mathematical concepts in understanding and solving problems across various disciplines. As we continue to delve into algebra, we find that seemingly disparate expressions can reveal profound connections and insights, enriching our understanding of the mathematical landscape.